No products in the cart.
High Impedance Busbar Differential Protection
We covered the basic operating principles of high impedance busbar differential protection in our previous post, I Want to Know How a High Impedance Differential Scheme Works. You should read that post first before we dig deep into the calculations and considerations that explain how high impedance busbar differential schemes function.
We received this question from the Ask Chris section at relaytraining.com. Follow this link to ask your own question and it might appear in a future blog post.
I had a lot of help with this question from Rodney Hughes at Rod Hughes Consulting Pty Ltd (www.rodhughesconsulting.com). His explanations are much more comprehensive than this one and I highly recommend you visit his website to really dig into it.
High Impedance Busbar Protection Principles and Calculations
The previous article left off with a single line drawing of our busbar protection.
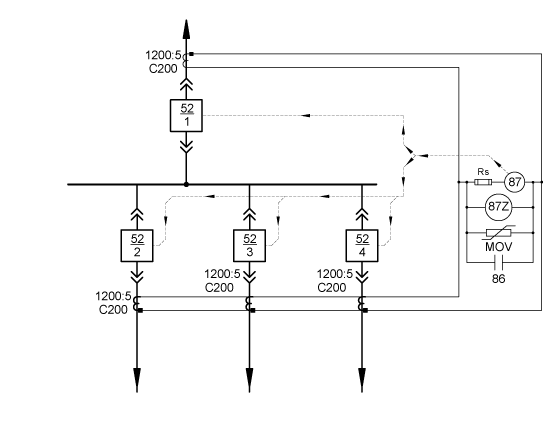
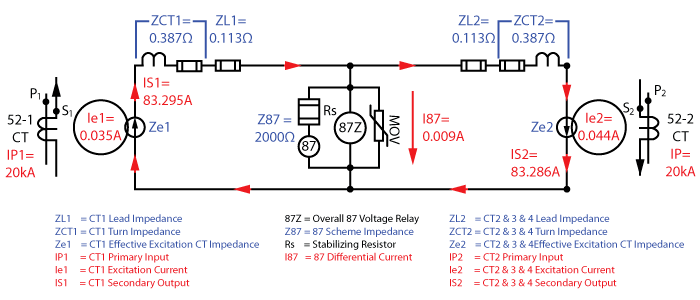
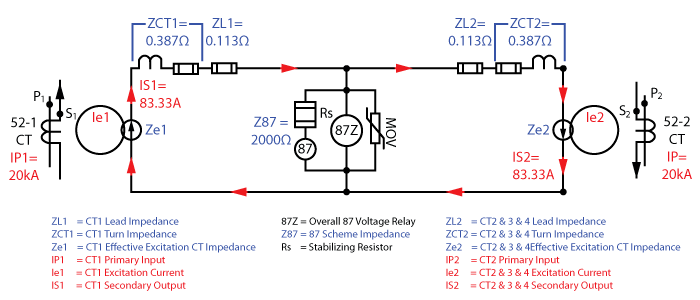
The equivalent circuit of this busbar protection scheme would look like the following:
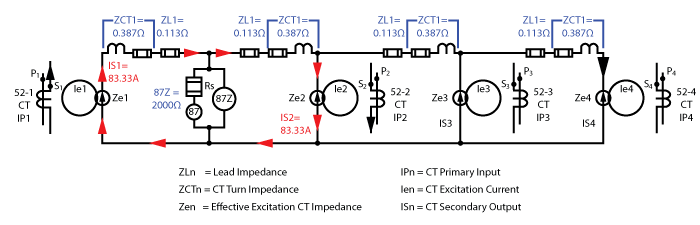
That is far too complicated for our purposes. We can combine 52-2 CT, 52-3 CT, and 52-4 into one CT to simplify the circuit to look like the following:
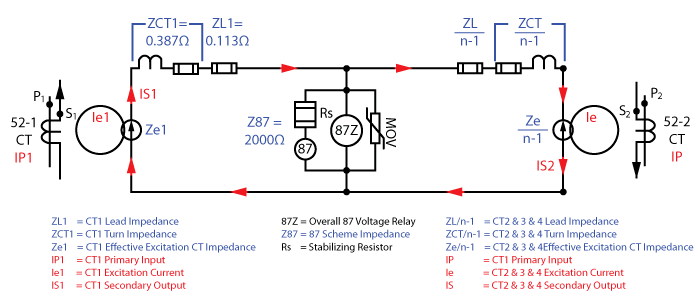
But we’re going to apply an external fault through two feeders to make it easier to understand.
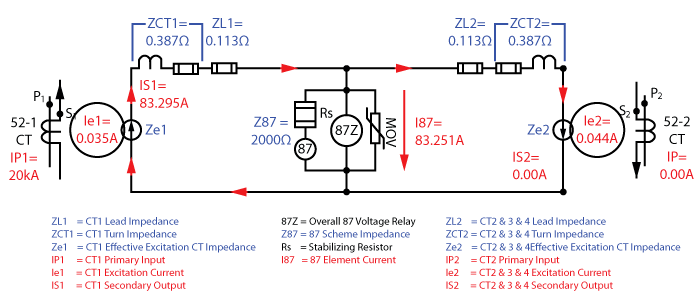
Any current flowing through the 52-1 CT (52-1CT IP1) is shown on the left hand side of our two-feeder equivalent circuit below. The primary current creates a magnetic field (Ie1, Ze1) that usually uses a small amount of current to inject the secondary current (IS1) into the CT secondary circuit.
The secondary winding is made from a conductor that has resistance and is coiled around a core to create inductance. That impedance is shown on the drawing as ZCT1. The external conductors connecting the CT to the rest of the circuit also have an impedance that is represented by ZL1.
Our high impedance busbar protective equipment has a 2000Ω impedance represented by the Rs, 87, 87Z, and MOV (Metal Oxide Varistor) in the middle of the circuit.
The 52-2 CT has the same characteristics as the 52-1 CT, which is represented on the right-hand side of the equivalent circuit. The CTs are connected in parallel with all polarity marks connected to the same point so that external faults theoretically cancel each other out, and internal faults combine to create larger currents during a fault for shorter trip times.
What Happens Inside a High Impedance Busbar Protection Scheme During an External Fault When One CT Saturates?
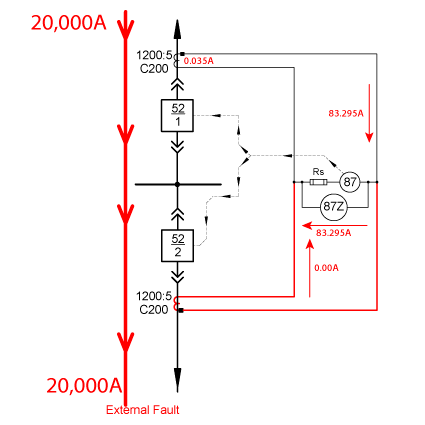
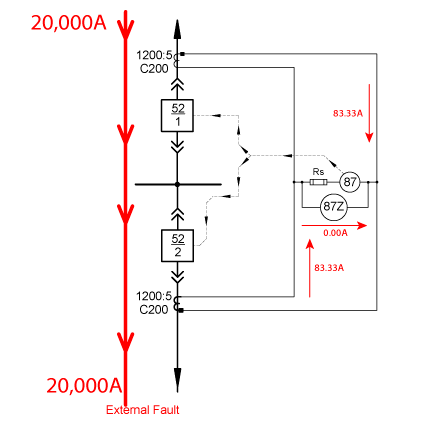
This scenario is THE reason why busbar protection can’t use simple instantaneous overcurrent elements (50). We have the same fault current as the ideal example in the previous single line drawing, but the 52-2 CT has saturated. The CT could have saturated because of:
- The DC Offset that commonly occurs during faults (You can get more info in the What is DC Offset? Ask Chris post)
- Residual magnetism in the CT (Remanence) from previous faults or improper testing
- Too much burden on the CT secondaries
A normal CT has a CT ratio (1200:5 in our example), which defines the turns-ratio (240:1 in our example). 83.33 should be exported When 20,000A flows through the 240 turns in a properly functioning CT, but:
- A normally insignificant amount of excitation current (0.035A) is used to create a magnetic field inside the CT to maintain the current transformation, which means
- 83.295A is injected out of the CT secondary terminals. (The actual CT ratio may be slightly higher than the reported 240:1 to compensate for the excitation current losses.)
When a CT saturates, the magnetic field requires more current than normal to maintain the current transformation, which means that there is less current injected into the CT secondary circuit. We’re showing the worst case scenario in our example where ALL of the primary current is used in the magnetic field, and zero amps is injected into the CT secondaries.
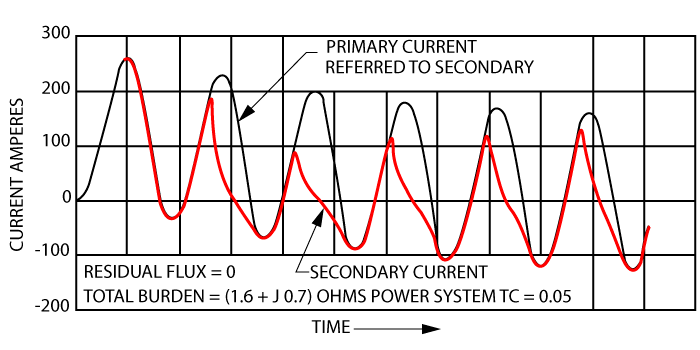
One hundred percent CT saturation is rare because the waveform becomes distorted when a CT saturates (as shown below), and most CTs will have varying degrees of saturation throughout a cycle, which makes the math in our equivalent circuit extremely difficult. Therefore, most high impedance busbar differential protection calculations use extremes to make the math easier.
High Impedance Busbar Differential Protection Maximum Voltage Calculation
The high impedance differential busbar protection has an impedance of 2000Ω. That means that the current will want to flow around the outside of the equivalent circuit because the outside circuit has a lower impedance path during external faults. When 52-2 CT fully saturates, its magnetic field impedance is effectively 0.00Ω. Let’s see what that does to our equivalent circuit.
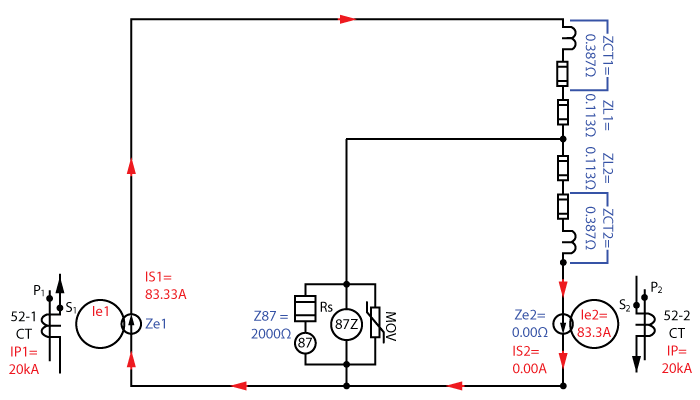
We can combine the ZCT1 and ZL1 impedance to get Z1 = 0.5Ω (0.387Ω + 0.113Ω). Then we can simplify the ZL2, ZCT2, and Ze2 impedances to get Z2 = 0.5Ω (0.387Ω + 0.113Ω + 0.00Ω).
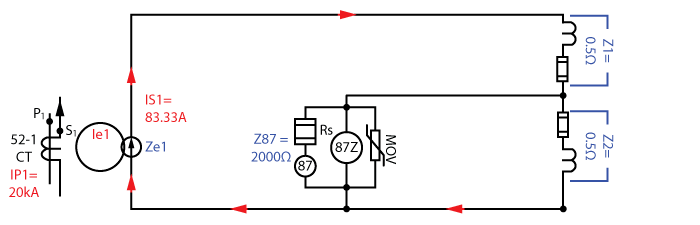
We can combine the Z2 and Z87 impedances to get 0.5Ω (2000Ω*0.5Ω / (2000Ω+0.5Ω)).
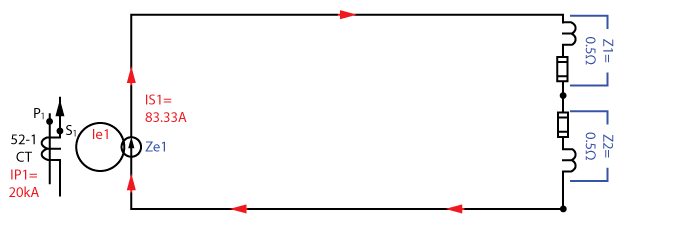
The equivalent circuit impedance for the 52-1 CT is 1.0Ω when 52-2 CT is saturating. Using Ohm’s Law, the voltage across 52-1 CT’s magnetic field with 83.33A of fault current is 83.33V.
Anyone designing or creating settings for a high impedance busbar differential protection scheme should calculate the maximum voltage that will be applied during an external fault with a 100% saturated CT as we just did in our example. We will use this maximum voltage to make sure that the CTs are sized appropriately for the application. Our CTs must operate normally with a secondary voltage of 83.33V.
High Impedance Busbar Differential Protection Minimum Allowable CT Saturation Voltage Calculation
High impedance busbar differential protection will not work properly if the CTs are not sized correctly for the connected circuit. We calculated that the voltage across the non-saturated CT, when another CT saturates, is 83.33V. Any CT with a saturation voltage greater than 83.33V should work correctly in our example. However, electrical engineers should always err on the side of caution when designing protection schemes; so we usually double the high impedance busbar differential protection maximum voltage calculation to determine the minimum CT saturation voltage to make sure that the CTs are adequately sized for the application. Our CTs should operate normally when 166.66V (2 * 83.33V) appears across the secondary terminals to be safe.
CT Ratings
A protection class CT is usually defined by its ratio, accuracy, construction, and burden. We’ve already discussed the CT ratio (1200:5 in our example). If you look back to the single line drawing, you’ll see that there was another designation beside the CTs (C200).

This designation defines:
- The accuracy class in percent (10% if no number appears in front of the letter)
- How the CT was constructed using a letter (C = Minimum leakage flux and CT performance can be calculated)
- The burden and saturation voltage in volts (200)
How can a voltage define the burden, you might ask? All standard protection class CT ratings are valid between 1 to 20x nominal current. If our CT’s have 5A nominal secondary currents, they are allowed to be +/-10% accurate between 5 and 100A secondary. If the maximum burden is 200V, we can apply Ohm’s Law to determine that the maximum impedance connected to the CT secondaries is 2.0Ω (200V / 100A). That’s the standard calculation that ALL CT testers should know and apply when they are performing their CT tests. Did you?
All protection class CTs also have a saturation curve like the graph below. The 200 in our rating means that if the voltage across the CT’s magnetic field is greater than 200V, the CT is no longer guaranteed to operate within its 10% error. 200V is greater than 166.66V (our minimum allowable CT saturation voltage), so the CTs in our example are appropriate for our application.
Determine CT Excitation Current
We can use the CT saturation curve to see how much excitation current will be used to maintain the current transformation at 83.33V with these steps:
- Start by drawing a horizontal line from 83.33V until you reach the 1200:5 curve.
- Then draw a vertical line to the secondary excitation current x-axis.
- Determine the excitation current using the log scale on the x-axis (0.035A).
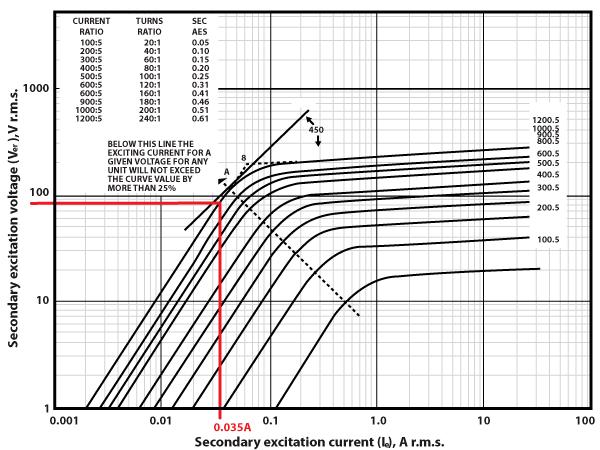
It is important to remember that this curve is a generic one, which gives an approximation of what the CT characteristic should be, and not what it actually is. Our class C CTs have a +/- 10% accuracy rating and when we get numbers from this curve, there may be significant differences between the information we calculate or obtain from the graph compared to actual CT operation. We would have to isolate every CT in the circuit and measure their performance to get exact performance numbers; or the design engineer could order a special class X CT where the performance characteristics are built and measured to ensure they meet exacting specifications.
Rodney Hughes (www.rodhughesconsulting.com) stresses that every high impedance busbar differential scheme should use class X CTs with exacting specifications to make sure we don’t get false trips due to CT mismatch. If you use class X CTs, you don’t have to worry that your CTs from the 1980s might not have the same operating characteristics as the new feeder CTs added to the scheme in the 2010s; they should have almost identical operating characteristics. The same CANNOT be said for standard class C CTs.
We don’t have the luxury of class X CTs in our example, so we’re going to use the excitation current (0.035A) we measured from the graph for all future calculations. The excitation voltage across the CTs will be less under normal conditions, but we don’t want to constantly go back and forth to this chart for every scenario. The chart states that the excitation current won’t exceed 25%; so let’s use 0.035A (our number from the graph) for CT1 and 0.044A (0.035 * 1.25) for CT2.
What Happens Inside a High Impedance Busbar Protection Scheme During an External Fault Without CT Saturation?
The following single line shows an external fault with CTs that are functioning as per the excitation graph.
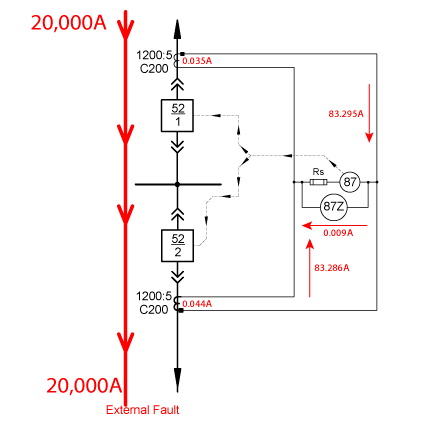
We have 20,000A flowing into the primaries of the CTs in the opposite direction. A perfect CT would send 83.33A into the secondary circuit, but the CTs’ magnetic field requires some current to make the current transformation (0.035A and 0.044A); so the actual CT output is 83.295A for 52-1 CT, and 83.286A for 52-2 CT. (The CT would normally have some hidden turns added to compensate for the excitation current.) The difference in CT secondaries creates a differential current of 0.009A that flows through the high impedance busbar differential circuit. We can apply Ohm’s Law to calculate 18.00V across the 87Z high impedance busbar protection circuit. This means that the 87Z pickup setting must be greater than 18.00V to prevent mis-operations during external faults. (The differential current would likely be higher in the real world due to CT mismatch.)
What should the high impedance busbar differential voltage setting be?
High Impedance Busbar Differential Protection Minimum Pickup Setting Calculation
The high impedance busbar differential protection scheme’s minimum pickup setting is calculated using our first scenario with the saturated CT.

We can re-organize and simplify the equivalent circuit to:

How much voltage is across the 87Z element in this scenario?
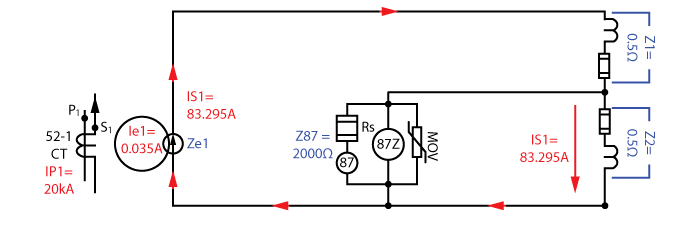
The 87Z element is in parallel with Z2. The 87Z circuit has a much higher impedance compared to the Z2 impedance, which makes the equivalent impedance almost 0.5Ω. We can use Ohm’s Law to calculate that there will be 41.65V (83.295A * 0.5Ω) across Z2 and 87Z during this scenario. Remember, we DO NOT want the relay to trip for external faults; so the setting should be higher than 41.65V.
Let’s imagine that we set the relay to 50V. We can calculate how much differential current will cause the relay to trip under normal conditions using Ohm’s Law. The 87Z is 2000Ω in our example with a 50V setting. That means that 0.025A (50V / 2000Ω) of differential current will cause the relay to trip. This setting might be OK with class X CTs with specific operating characteristics, but we will probably get a false trip with normal class C CTs, especially if we have different vintages of CTs in our high impedance busbar differential circuit.
Most design engineers add a safety factor starting at 1.5x the minimum setting to account for potential increases in fault current. We will increase the setting by a factor of two and then round up to 100V. This means that the differential current caused by CT mismatch (0.05A or 100V/2000Ω) must be twice our previous setting, or higher, to cause a mis-operation during normal conditions or through-faults.
What Happens Inside a High Impedance Busbar Protection Scheme During an Internal Fault With One Source?
Here is a single line displaying what happens during an internal fault.
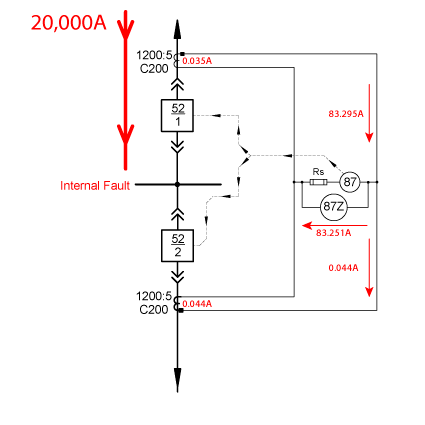
We have 20,000A flowing into the 52-1 CT which should equal 83.333A flowing out of its secondary terminals. However, the CT needs excitation current to create secondary current. If we use our previously calculated 0.035A for this scenario (that amount would not technically apply here, but we need to pick something and I don’t want to do more math for such a small amount of current), 83.295A should flow out of the CT secondaries.
Since the 52-2 CT has zero amps flowing in the primary windings, zero amps should flow out of the secondaries. Without a magnetic field however, the 52-2 CT’s secondary winding is just a bunch of coiled wire with a low impedance. The 52-1 CT secondary current will want to flow through the low impedance in the 52-2 CT secondaries, but once a small amount of current (0.044A from our previous example) starts flowing in the secondary circuit, a magnetic field will be created and the CT will try to maintain its turns-ratio. Zero amps of the primary should equal zero amps on the secondary minus the excitation current. Once the magnetic field is built, the 52-2 CT secondaries will become an open circuit (like it does when you perform your saturation and ratio tests) and the remaining current will flow through the 87Z circuit because it will now have a lower impedance.
Using Ohm’s Law, 83.251A through 2000Ω should create 166,502V. The MOV will protect the secondary circuits from damage by limiting the possible voltage to a number much smaller than 166,502V, but the secondary voltage could rise to the system voltage without the MOV. Either way, it is extremely unlikely that the voltage will reach those heights because the CT should start saturating at 200V. The CT is guaranteed to saturate during an internal fault and will produce a waveform that looks like this:

Our relay better be able to operate when this waveform appears; so it is often beneficial to use a single-purpose relay for a high impedance busbar differential relay scheme to minimize the trip time. Some digital relays need extra time to measure, apply filters, and analyze the waveform before they can operate, which may mean that the fault may stay on the system longer than necessary. The longer a fault stays on the system, the greater potential for system de-stabilization, which could cause a larger system outage than necessary.
The voltage during an internal fault should always be larger than our setting and the relay should trip in the shortest time possible.
What Happens Inside a High Impedance Busbar Protection Scheme During an Internal Fault With Multiple Sources?
Most distribution busses have multiple sources and we should look at this scenario to see what happens:
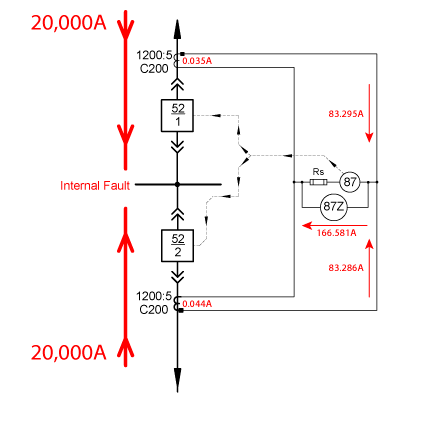
The CT secondary currents are headed in the same direction in this scenario and will combine at the 87Z circuit to theoretically produce 333,162V (166.581A * 2000Ω). Both CTs will drive the highest voltage they can while in parallel, which will trip the relay.
Conclusion
The dirty little secret about all forms of differential protection is that we know the relay will trip for all internal faults. When we’re designing and testing differential schemes, we’re primarily concerned with making sure the relay will NOT trip during external faults. Did you notice that all of the important calculations above occurred during external fault scenarios? Have you noticed that most differential tests try to find the point where the relay will operate during an external fault (currents 180° apart), instead of applying single source or multiple source fault in the same direction?
High impedance differential schemes can filter out non-sinusoidal differential current that occurs when CTs saturate during external faults, but they cannot filter out true error caused by CT mismatch. Therefore, it is important that you use class X CTs when you are designing high impedance differential schemes, and that you are aware that CT mismatch can cause mis-operations when using standard protection class CTs.
I hope this article helped you better understand high impedance differential schemes. If you liked it, please share it to help us get noticed, which helps us continue to produce free content like this.
Did you like this post?
You can share it with these links:
Read More Articles:
What Was Your Electrical Epiphany?

Great article thanks for taking the time to create graphics and breaking each section down etc – Concepts explained well which made it easy to understand how this form of protection works.
Thanks!
Thank you very much.
Great article. I am working on a scheme where the bus differential setting is 300V where as the CTs used are all identical C200s. Any concerns here? Most articles I have read always reference the setting to be below the saturation list of the CT…this scheme does not do that. Your time is appreciated.
Thanks for the question.
C200 CTs do not have a lot of oomph, so they are not recommended for high impedance bus differential. These CTs would only be appropriate if the entire scheme was within 4-6 switchgear cells, and you would be pushing their limitations at that.
The maximum CT secondary voltage under normal conditions would be slightly above 200V. If your scheme is 300V, it will probably never operate.
Hi Chris… your explanation is very good. Easy to understand. Thank you,
Referring to the equivalent circuit diagram after
“The equivalent circuit of this busbar protection scheme would look like the following:”
I couldn’t understand, why the ZCT in series with the ZL? From my understanding it (ZCT) should series with Ze
Thanks again…
Thanks for the question. ZCT is in series with Ze. Think of Ze as a perfect voltage source with 0 ohms impedance. The voltage it creates will be applied tot he internal impedances of the CT (ZCT), the wiring to the load (ZL1), and the load to make a complete load for the perfect source.
Firstly, many thanks for your effort, I have one question, what will be happen if a CT is saturated during internal fault?
The CT would have saturated because the secondary voltage was too high. The design engineer should have performed the calculation to determine what that minimum voltage should be and set the high impedance-differential below that value. Therefore, the scheme would trip.
What will happen if one CT during internal faults becomes saturated???
Why would it matter if a CT saturates during an internal fault?
Understood, Thanks.
One more question
Although it is not recommended to use Matching CTs if one of feeder CT has different CT ratio than the other Feeder CTs.
But let say if one feeder CT ratio is different than the others and we have used Matching CT to make the scheme stable.. What will be the issues?? and why it is not recommended to use Matching CTs?
The matching CT’s impedance and operating characteristics will be nothing like the other CTs, therefore, there will be a lot of CT mismatch that could cause nuisance trips. The High impedance scheme only needs a tiny amount of mismatch current to trip.
Thanks Mr. Chris. :)
As you have said that using Matching CT in one feeder will cause nuisance tripping and that is understanable and this nuisance tripping will be mostly in the case of external fault. But however one utility has used matching CT to make the high impedance scheme stable.
In this regard I have a question that in one of your example in the article where you have considered internal fault with one source and if matching CT has been used for CT associated with 52/2 Breaker (in which no current is flowing) due to different CT ratio. then in this case will the relay trip incase of internal fault ??
as per my understanding , the matching CT will saturate (if low quality matching CT has been used or the matching CT has lost its property due to certain reason) and now the current which have to be passed through the relay coil in case of internal fault will flow towards the saturated matching CT? am I right? thus there will be no tripping during internal faults. kindly clarify
thanks for bearing my question in advance
I’m not sure why you are so concerned about internal faults.
If a tiny bit of unbalance current CAN cause nuisance trips, an internal fault would provide current off the charts if it wasn’t connected to a high impedance. The CT is guaranteed to saturate in an internal fault, and a saturated CT creates low current/high voltage…the very voltage that the high-impedance scheme operates on.
Mr Chris i have one question
we take one CT fully saturate for an external fault.. then why in this case voltage is not developing across the sexondary side of CT?
Voltage HAS to develop across the secondary of a saturated CT. The reason why the CT is saturated is because there is too much voltage across the secondary.
the voltage in case of internal fault will be very high but why this voltage in the case of saturated CT due to external fault is not so high? what is the reason for this?
Because there is high differential current during an internal fault and theoretically none in an external fault.
Great explanation. But I could not understand why a CT under saturation behave as one with zero magnetic impedance. Also why during the internal fault,52-2 CT secondaries behave as open circuit. Can you please elaborate it bit further.